Sorting Algorithms | Programming and Data Structures | Realcode4you

realcode4you

5 hours ago5 min read

In this post we will learn about three important sort algorithms which is given below:

Insertion sort
Selection sort
Bubble sort

Insertion sort

Have a look at this example, can you figure out the process of insertion sort?

Insertion sort

At each round i: {item 0, item 1, …, item i} are sorted

helicopter view pseudocode of Insertion Sort Algorithm of a list of integers

n = length-of(intList) 
FOR i from 1 to (n-1) 
	// sort intList[0], intList[1], …, intList[i] 
END FOR

Look at each round in details:

helicopter view pseudocode of Insertion Sort Algorithm of a list of integers

n = length-of(intList) 
FOR i from 1 to (n-1) 
	// sort intList[0], intList[1], …, intList[i] 
END FOR

At each round i: {item 0, item 1, …, item i} are sorted

pseudocode of round i

 // sort intList[0], intList[1], …, intList[i] 
k = i 
WHILE k > 0 and intList[k-1] > intList[k] 
	swap intList[k] and intList[k-1] 
	k = k - 1 
END WHILE

Put it together, we have the algorithm for Insertion Sort:

pseudocode

n = length-of(intList) 
FOR i from 1 to (n-1) 
	// sort intList[0], intList[1], …, intList[i] 
	k = i 
	WHILE k > 0 and intList[k-1] > intList[k] 
		swap intList[k] and intList[k-1] 
		k = k - 1 
	END WHILE 
END FOR

Python implementation

def insertionSort(intList):
   n = len(intList)
   for i in range(1, n):
   #{
       # sort intList[0], intList[1], ..., intList[i]
       k = i
       while (k > 0) and (intList[k-1] > intList[k]):
       #{
           # swap intList[k] and intList[k-1]
           temp = intList[k]
           intList[k] = intList[k-1]
           intList[k-1] = temp
           k = k - 1
       #}
   #}

Suggested activities:

Make up a list of integers and write down in details each step in sorting this list of integers;
Sort a list of integers in descending order;
Sort a list of decimal numbers;
Sort a list of strings

Python List

A list/array is used to hold a list of items:

animal_list = ["dog", "cat", "frog"] 
fibo_numbers = [0, 1, 1, 2, 3, 5, 8, 13] 
prime_numbers = [2, 3, 5, 7, 11, 13, 17]
subject_list = ["MATH101", "CS222", "PHY102", "ACCY203"] 
selected_products = [] # this is an empty list

This is how we define a list:

list_variable = [item1, item2, …, itemN]

List items can be accessed via index:

fibo_numbers = [0, 1, 1, 2, 3, 5, 8, 13] 

print(fibo_numbers[0])  → 0
print(fibo_numbers[1])  → 1
print(fibo_numbers[2])  → 1
print(fibo_numbers[3])  → 2
print(fibo_numbers[4])  → 3
print(fibo_numbers[5])  → 5
print(fibo_numbers[6])  → 8
print(fibo_numbers[7])  → 13

items can be appended to the end of the list:

 fibo_numbers.append(21) 
 fibo_numbers.append(34)
 fibo_numbers.append(55)
 fibo_numbers.append(89)

using len to find out how many items in the list:

animal_list = ["dog", "cat", "frog"] 
animal_count = len(animal_list) → 3

Note that len(animal_list) is 3, but the last index is 2 because the index start at 0

print(animal_list[0])   → "dog"
print(animal_list[1])   → "cat"
print(animal_list[2])   → "frog"

Selection sort

Have a look at this example, can you figure out the process of selection sort?

At each round i: find the minimum in {item i, item i+1, … } and swap it to the position i

Look at each round in details:

Algorithm for Selection Sort:

pseudocode

n = length-of(intList)
 FOR i from 0 to (n-2)
   among intList[i], intList[i+1], …, intList[n-1]
   find the minimum item intList[kMin]
   swap intList[i] and intList[kMin]
 END FOR

Python Implementation

def selectionSort(intList):
    n = len(intList)
    for i in range(0, n-1):
    #{
        # find the minimum item in intList[i .. n-1]
        kMin = i
        for k in range(i+1, n):
            if (intList[k] < intList[kMin]):
                kMin = k
        # swap intList[i] and intList[kMin]
        if (kMin != i):
            temp = intList[i]
            intList[i] = intList[kMin]
            intList[kMin] = temp
    #}

Bubble sort

Bubble (up) sort algorithm:

Go through the list, compares adjacent items and swaps them if they are in the wrong order;
Repeat this process until the list is sorted.

The name of the algorithm is derived from the fact that: after each round, the largest items are bubbled up towards the end of the list.

Let’s look at each round in details: (compares adjacent items and swaps them if they are in the wrong order)

Observe the movement of the largest item 100

We can see that after the 1st round, the largest item 100 is bubbled up to the end of the list.

We can see that after the 2st round, the 2nd largest item 90 is bubbled up to the right place towards the end of the list.

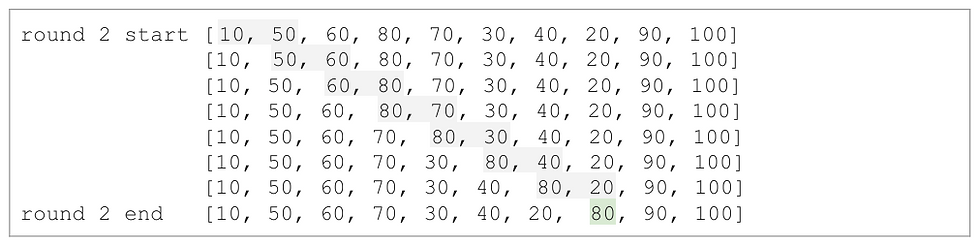
We can see that after the 3rd round, the 3rd largest item 80 is bubbled up to the right place towards the end of the list.

We can see that after the 4th round, the 4th largest item 70 is bubbled up to the right place towards the end of the list.

After the 5th round, the 5th largest item 60 is bubbled up to the right place towards the end of the list.

After the 6th round, the 6th largest item 50 is bubbled up to the right place towards the end of the list.

After the 7th round, the 7th largest item 40 is bubbled up to the right place towards the end of the list.

After the 8th round, the 8th largest item 30 is bubbled up to the right place towards the end of the list

After the 9th round, the 9th largest item 20 is bubbled up to the right place towards the end of the list - and the sorting is DONE!!!

pseudocode

n = length-of(intList)
 FOR i from 0 to (n-2)
    FOR j from 1 to (n-i-1)
        // compare adj items, swap if in wrong order
        IF intList[j-1] > intList[j]:
            swap intList[j-1] and intList[j]
        END IF
    END FOR
 END FOR

Python implementation

def bubbleSort(intList):
    n = len(intList)
    for i in range(0, n-1):
    #{
        for j in range(1, n-i):
        #{
            # compare adj items, swap if in wrong order
            if intList[j-1] > intList[j]:
                # swap intList[j-1] and intList[j]
                temp = intList[j-1]
                intList[j-1] = intList[j]
                intList[j] = temp
        #}
    #}

Notice that in round 2, NOT a single swap is needed. It means that the list has already been sorted. NO NEED TO GO ANY FURTHER TO round 3, round 4, round 5, ..

Better algorithm:

pseudocode

n = length-of(intList)
 FOR i from 0 to (n-2)
    swapped = false
    FOR j from 1 to (n-i-1)
        // compare adj items, swap if in wrong order
        IF intList[j-1] > intList[j]:
            swap intList[j-1] and intList[j]
            # remember that swap is needed
            swapped = true 
        END IF
    END FOR
    BREAK IF swapped = false
 END FOR

Python implementation

def bubbleSort(intList):
    n = len(intList)
    for i in range(0, n-1):
        swapped = False
        for j in range(1, n-i):
            # compare adj items, swap if in wrong order
            if intList[j-1] > intList[j]:
                # swap intList[j-1] and intList[j]
                temp = intList[j-1]
                intList[j-1] = intList[j]
                intList[j] = temp
                # remember that swap is needed
                swapped = True  
        if not swapped:
            # swap is NOT needed, so list is SORTED
            break

Suggested activities:

Make up a list of integers and write down in details each step in sorting this list of integers;
Sort a list of integers in descending order;
Write a Bubble (down) sort algorithm, so that after each round, the smallest items are bubbled down towards the start of the list;
Write a program to generate a random list of integers of length N;
Write a program to count how many comparison operations, and how many swap operations are needed to sort this random list using each sorting algorithms;
Repeat this program many times with a large sample of random lists of integers and display the statistics.

References

● Python 3 documentation https://docs.python.org/3/

● NumPy Reference https://numpy.org/doc/stable/reference/

RealCode4You

Sorting Algorithms | Programming and Data Structures | Realcode4you

Recent Posts

Comments