Linear Regression With K-fold Cross Validation Using Sklearn and Without Sklearn

With Sklearn

In this post we will implement the Linear Regression Model using K-fold cross validation using the sklearn.

Import Necessary Libraries:

#Import Libraries
import pandas
from sklearn.model_selection import KFold
from sklearn.preprocessing import MinMaxScaler
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import LabelEncoder

Read abalone Dataset

#Read Dataset
dataset = pandas.read_csv('abalone.csv')
dataset

Output:

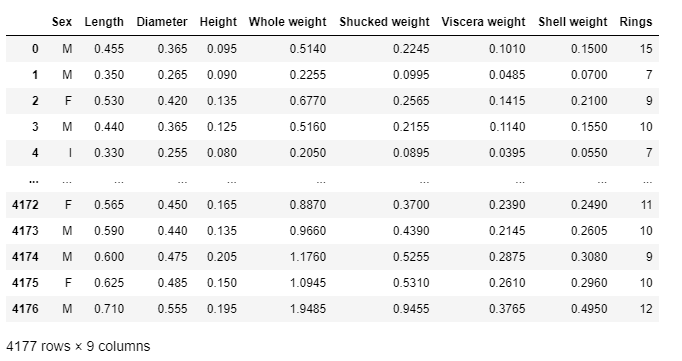
Encode the categorical variable

#label encoder to change the string object into the numeric 
label_encoder = LabelEncoder()
dataset['Sex'] = label_encoder.fit_transform(dataset['Sex'])

Selecting Target And Feature Variable

X = dataset.iloc[:, [0, 7]]
y = dataset.iloc[:, 8]

Fit into model using K-fold

X = dataset.values.astype(np.float)
# fit the estimator to the data
scores = []
model = LinearRegression()
cv = KFold(n_splits=5, random_state=42, shuffle=True)
for train_index, test_index in cv.split(X):
    print("Train Index: ", train_index, "\n")
    print("Test Index: ", test_index)

    X_train, X_test, y_train, y_test = X[train_index], X[test_index], y[train_index], y[test_index]
    model.fit(X_train, y_train)
    scores.append(model.score(X_test, y_test))

Output:

Find the Score

print(np.mean(scores))

Find the Cross Validation

from sklearn.model_selection import cross_val_score
cross_val_score(model, X, y, cv=5)

Without Sklearn

Here we have implement it without sklearn and last we will find the accuracy.

class LinearRegression:
    '''
    A class which implements linear regression model with gradient descent.
    '''
    def __init__(self, learning_rate=0.01, n_iterations=10000):
        self.learning_rate = learning_rate
        self.n_iterations = n_iterations
        self.weights, self.bias = None, None
        self.loss = []
        
    @staticmethod
    def _mean_squared_error(y, y_hat):
        '''
        Private method, used to evaluate loss at each iteration.
        
        :param: y - array, true values
        :param: y_hat - array, predicted values
        :return: float
        '''
        error = 0
        for i in range(len(y)):
            error += (y[i] - y_hat[i]) ** 2
        return error / len(y)
    
    def fit(self, X, y):
        '''
        Used to calculate the coefficient of the linear regression model.
        
        :param X: array, features
        :param y: array, true values
        :return: None
        '''
        # 1. Initialize weights and bias to zeros
        self.weights = np.zeros(X.shape[1])
        self.bias = 0
        
        # 2. Perform gradient descent
        for i in range(self.n_iterations):
            # Line equation
            y_hat = np.dot(X, self.weights) + self.bias
            loss = self._mean_squared_error(y, y_hat)
            self.loss.append(loss)
            
            # Calculate derivatives
            partial_w = (1 / X.shape[0]) * (2 * np.dot(X.T, (y_hat - y)))
            partial_d = (1 / X.shape[0]) * (2 * np.sum(y_hat - y))
            
            # Update the coefficients
            self.weights -= self.learning_rate * partial_w
            self.bias -= self.learning_rate * partial_d
        
        
    def predict(self, X):
        '''
        Makes predictions using the line equation.
        
        :param X: array, features
        :return: array, predictions
        '''
        return np.dot(X, self.weights) + self.bias
    
    def accuracy_metric(actual, predicted):
        correct = 0
        for i in range(len(actual)):
            if actual[i].all() == predicted[i].all():
                correct += 1
        return correct / float(len(actual)) * 100.0

Read DataSet And Find Accuracy

import pandas as pd
import numpy as np
df = pd.read_csv('abalone.csv')
model = LinearRegression()

#Selecting Target Variable
y = df.Rings.values
del df["Rings"]

#Use Label Encoder to change string data into numeric
import sklearn
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
df['Sex'] = label_encoder.fit_transform(df['Sex'])

#Split Dataset
X = df.values.astype(np.float64)
# fit the estimator to the data
from sklearn.model_selection import train_test_split
train_X, test_X, train_y, test_y = train_test_split(X, y) 

# apply the model to the test and training data
predicted_test_y = model.predict(test_X)
predicted_train_y = model.predict(train_X)

# Test accuracy
actual = test_X
predicted = predicted_test_y
accuracy = accuracy_metric(actual, predicted)
print(accuracy)

If you need any machine learning algorithms related help which is related to supervised or unsupervised machine learning then send your request or requirement details at:

realcode4you@gmail.com

And get instant help with an affordable price.